6.3 Metodo de Pasos Multiples

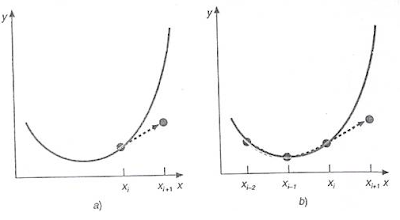
Los métodos de un paso descritos en las secciones anteriores utilizan información en un solo punto xi para predecir un valor de la variable dependiente yi+1 en un punto futuro xi+1. Procedimientos alternativos, llamados métodos multipaso, se basan en el conocimiento de que una vez empezado el cálculo, se tiene información valiosa de los puntos anteriores y esta a nuestra disposición. La curvatura de las líneas que conectan esos valores previos proporciona información con respecto a la trayectoria de la solución. Los métodos multipaso que exploraremos aprovechan esta información para resolver las EDO. Antes de describir las versiones de orden superior, presentaremos un método simple de segundo orden que sirve para demostrar las características generales de los procedimientos multipaso.

Observe la ecuación ec. 2  alcanza ) a expensas de emplear un tamaño de paso mas grande, 2h. Además, observe que la ecuación ec. 1 no es de autoinicio, ya que involucra un valor previo de la variable dependiente yi-1. Tal valor podria no estar disponible en un problema común de valor inicial. A causa de ello, las ecuaciones 26.11 y 26.12 son llamadas método de Heun de no autoinició.

Como se ilustra en la figura 26.4, la derivada estimada de la ecuación 26.12 se localiza ahora en el punto medio mas que al inicio del intervalo sobre el cual se hace la predicción. Como se demostrara después, esta ubicación centrada mejora el error del predictor a  Sin embargo, antes de proceder a una deducción formal del método de Heun de no autoinicio, resumiremos el método y lo expresaremos usando una nomenclatura ligeramente modificada:

La ecuación se puede aplicar de manera iterativa hasta que Ea esté por debajo de un valor pre especificado de Es. Como fue el caso con el método de Heun, las iteraciones convergen sobre un valor de 6.360865. Sin embargo, como el valor del predictor inicial es más exacto, el método de multipaso converge una razón algo más rápida.
Para el segundo paso, el predictor es:

Que es superior a la predicción de 12.08260 que fue calculada con el método de Heun original. El primer corrector da 15.76693 e iteraciones subsecuentes convergen sobre el mismo resultado como se obtuvo con el método de Heun de autoinicio: 15.30224. Como con el paso anterior, la razón de convergencia del corrector ha sido mejorada debido a la mejor predicción inicial.

Deducción y análisis del error de las formulas del predictor-corrector. Ya empleamos conceptos

gráficos para deducir el Heun de no autoinicio. Ahora mostraremos como las mismas ecuaciones se pueden deducir matemáticamente. Esta deducción es en particular interesante porque vincula las ideas del ajuste de curva, de la integración numéricas y de las EDO. El ejercicio también es útil porque proporciona un procedimiento simple para desarrollar métodos de multipaso de orden superior y estima sus errores.
La deducción se basa en resolver la EDO general:

La ecuación representa una solución a la EDO si la integral puede ser evaluada. Es decir, proporciona un medio para calcular un nuevo valor de la variable dependiente  con base en un valor previo de  y la ecuación diferencial.
Las formulas de integración numérica proporcionan una manera de hacer esta evaluación. Por ejemplo, la regla trapezoidal se puede usar para evaluar la integral, como en:

El cual es el predictor para el Heun de no autoinicio. Como con el corrector, el error de truncamiento local se puede tomar directamente:

Donde el subíndice p designa que este es el error dele predictor.
Así, el predictor y el corrector para el método de Heun de no autoinicio tiene errores de truncamiento del mismo orden. Además de actualizar la exactitud del predictor, este hecho tiene beneficios adicionales relacionados con el análisis del error, como se elaborara en la siguiente sección.
Estimación de errores: Si el predictor y el corrector de un método multipaso son del mismo orden, el error de truncamiento local puede estimarse durante el curso de un cálculo. Esto es una tremenda ventaja, ya que establece un criterio para el ajuste del tamaño de paso.
El error de truncamiento local para el predictor se estima con la ecuación ec.9. Dicho error estimado se puede combinar con el estimado de  del paso predictor para dar:

6.2 Métodos de un paso: Método de Euler, Método de Euler mejorado y Método de Runge-Kutta.

En matemática y computación, el método de Euler, llamado así en honor de  Leonhard Euler, es un procedimiento de integración numérica para resolver  ecuaciones diferenciales ordinarias a partir de un valor inicial dado. El método de Euler es el más simple de los métodos numéricos resolver un problema  del siguiente tipo: Grafica A. Método de Euler Mejorado Este método se basa en la misma idea del método anterior, pero hace un refinamiento en la aproximación, tomando un promedio entre ciertas pendientes.  La fórmula es la siguiente:  Donde Para entender esta fórmula, analicemos el primer paso de la aproximación, con base en la  siguiente gráfica:   En la gráfica, vemos que la pendiente promedio   corresponde a la  pendiente de  la recta bisectriz de la recta tangente a la curva en el punto de la condición  inicial y la "recta tangente" a la curva en el punto   donde   es la aproximación obtenida con  la primera fórmula de Euler. Finalmente, esta recta bisectriz se traslada paralelamente   hasta el punto de la condición inicial, y se considera el valor de esta recta en  el punto    como la aproximación de Euler mejorada.  Método de Runge-Kutta El método de Runge-Kutta es un método genérico de resolución numérica de ecuaciones diferenciales. Este conjunto de métodos fue inicialmente desarrollado alrededor del año  1900 por los matemáticos C. Runge y M. W. Kutta. Los métodos de Runge-Kutta (RK) son un conjuntos de métodos iterativos (implícitos y explícitos)  para la aproximación de soluciones de ecuaciones diferenciales ordinarias, concretamente,  delproblema de valor inicial.

6.1 Fundamentos de ecuaciones diferenciales.

Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o  más funciones desconocidas. Dependiendo del número de variables independientes  respecto de las que se deriva, las ecuaciones diferenciales se dividen en Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una  sola variable independiente. §  Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos  o más variables. §  Una ecuación diferencial es una ecuación que incluye expresiones o términos que  involucran a una función matemática incógnita y sus derivadas. Algunos ejemplos de  ecuaciones diferenciales son: es una ecuación diferencial ordinaria, donde   representa una función no especificada de  la variable independiente  , es decir,  ,   es la derivada de   con respecto a  . §  La expresión  es una ecuación en derivadas parciales. A la variable dependiente también se le llama función incógnita (desconocida).  La resolución de ecuaciones diferenciales es un tipo de problema matemático  que consiste en buscar una función que cumpla una determinada ecuación  diferencial. Se puede llevar a cabo mediante un método específico para la ecuación  diferencial en cuestión o mediante una transformada (como, por ejemplo, la  transformada de Laplace). Orden de la ecuación El orden de la derivada más alta en una ecuación diferencial se denomina  orden de la ecuación. Grado de la ecuación Es la potencia de la derivada de mayor orden que aparece en la ecuación,  siempre y cuando la ecuación esté en forma polinómica, de no ser así se  considera que no tiene grado. Ecuación diferencial lineal Se dice que una ecuación es lineal si tiene la forma  , es decir: §  Ni la función ni sus derivadas están elevadas a ninguna potencia distinta de  uno o cero. §  En cada coeficiente que aparece multiplicándolas sólo interviene la variable independiente. §  Una combinación lineal de sus soluciones es también solución de la ecuación. §  Ejemplos: §   es una ecuación diferencial ordinaria lineal de primer orden, tiene como soluciones  , con k un número real cualquiera. §   es una ecuación diferencial ordinaria lineal de segundo orden, tiene como  soluciones  , con a y b reales. §   es una ecuación diferencial ordinaria lineal de segundo orden, tiene como  soluciones  , con a y b reales.

5.3 integracion con intervalos desiguales

5.3 integracion con intervalos desiguales

Cuando se tienen datos de experimentos, es com´un tener segmentos desiguales. La integral se eval´ua con una mezcla de las tres reglas. La regla de Simpson de 1/3 para un n´umero par de segmentos adyacentes del mismo tama˜no. La regla de Simpson de 3/8 para tres segmentos adyacentes del mismo tama˜no. La regla del trapecio para un segmento con ning´un otro segmento adyacente del mismo tama˜no.

Asumir los siguientes datos de la funci´on f (x) = 0.2 + 25x − 200x² + 675x³ − 900x⁴ + 400x⁵

Analizando los segmentos contiguos

·         Un segmento de tama˜no 0.12

·          Dos segmentos de tama˜no 0.10

·         Tres segmentos de tama˜no 0.04

·          Dos segmentos de tama˜no 0.10

·         Un segmento de tama˜no 0.06

·         Un segmento de tama˜no 0.10

 La integral se aproxima por secciones

La gráfica con los datos

Sustituyendo la integral de cada secci´on por la regla de integraci´on seg´un el n´umero de segmentos de cada secci´on se tiene;

5.2 Integración numérica: Método del trapecio, Métodos de Simpson 1/3 y 3/8

5.2 Integración numérica: Método del trapecio, Métodos de Simpson 1/3 y 3/8

REGLAS TRAPEZOIDALES. REGLA TRAPEZOIDAL SENCILLA. La regla del trapecio o regla trapezoidal es la primera de las fórmulas  cerradas de Newton-Cotes. Corresponde al caso en donde el polinomio de aproximación    es de primer orden. Regla del Trapecio. Este nombre se debe a la interpretación  geométrica que le podemos dar a la fórmula. El polinomio de interpolación para una tabla  que contiene dos datos, es una línea recta. La integral, corresponde al área bajo la línea  recta en el intervalo [a,b]  , que es precisamente el área del trapecio que se forma. En donde f1(x) corresponde a una línea recta que se representa como: El área bajo la línea recta es una aproximación de la integral de f(x) entre los  límites a y b: El resultado de la integración es:

• REGLA TRAPEZOIDAL DE SEGMENTOS MULTIPLES.

Una manera de mejorar la exactitud de la regla trapezoidal sencilla es la de dividir el intervalo de integración desde "a" hasta "b" en conjunto de segmentos y aplicar el método a cada uno de los segmentos.

En seguida se suman las áreas de los segmentos individuales y se obtiene la integral sobre el intervalo completo.

Por consiguiente, hay n segmentos de igual anchura:

Si a y b se igualan a x0 y a xn (puntos base igualmente espaciados), la integral total se representa como:

Sustituyendo la regla trapezoidal para cada una de las integrales, se obtiene:

agrupando términos 

usando la ecuación en la forma general, se obtiene:

• REGLAS DE SIMPSON.

Ademas de aplicar la regla trapezoidal con segmentos cada vez más finos, otra manera de obtener una estimación más exacta de una integral, es la de usar polinomios de orden superior para conectar los puntos.

A las formulas resultantes de calcular la integral bajo estos polinomios se les llama reglas de Simpson.

• REGLA DE SIMPSON DE 1/3.

---

La regla de Simpson de 1/3 resulta cuando se sustituye un polinomio de segundo orden en la ecuacion:

Si a y b se denominan como x0 y x2 , y f2 (x) se representa mediante un polinomio de Lagrange de segundo orden, entonces la integral es:

Despues de integrar y de reordenar terminos, resulta la siguiente ecuación:
  

• REGLA DE SIMPSON 1/3 DE SEGMENTOS MULTIPLES.

---

Asi­ como la regla trapezoidal, la regla de Simpson se mejora dividiendo el intervalo de integración en segmentos de igual anchura.

h=(b-a)/n

La integral total se representa como:

Sustituyendo la regla de Simpson en cada una de las integrales individuales se obtiene:

reordenando los terminos, se obtiene:

• REGLA DE SIMPSON DE 3/8.

---

De manera similar a la derivación de la regla trapezoidal y a la regla de Simpson de 1/3, se ajustan polinomios de Lagrange de tercer orden a cuatro puntos e integrar;

para obtener

En donde h=(b-a)/3. A esta ecuación se le llama regla de Simpson de 3/8 porque h es un múltiplo de 3/8. Esta es la tercera regla cerrada de integración de Newton-Cotes. 
  
 

• REGLA DE SIMPSON 3/8 MULTIPLES.

---

La regla de Simpson de 1/3 es, en general, el método de preferencia ya que alcanza exactitud de tercer orden con tres puntos en vez de los de cuatro puntos necesarios para la versión de 3/8.

No obstante, la regla de 3/8 tiene utilidad en aplicaciones de segmentos múltiples cuando el número de segmentos es impar.

Para una estimación de cinco segmentos una alternativa es la de aplicar la regla de Simpson de 1/3 a los primeros segmentos y la regla de Simpson de 3/8 a los últimos tres.

De esta manera, se obtiene una estimación con exactitud de tercer orden a través del intervalo completo.